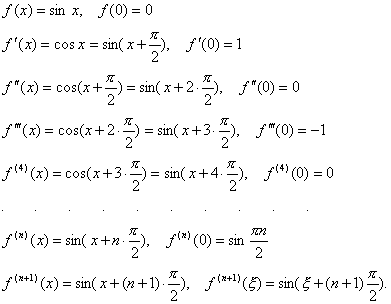Остаточный член разложения функции
Формула Тейлора с остаточным членом в форме Пеано. В случае функций, отличных от многочлена, формула 4 не справедлива. Однако если ограничиться значениями x , близкими к , то при определенных условиях можно утверждать, что аналог правой части 4 близок к функции. Теорема 1.


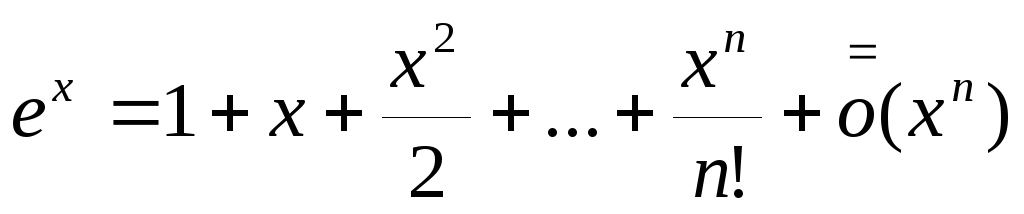








Дифференциальное исчисление функции одной переменной. Производные первого порядка. Определение производной.
- В дальнейшем нам пригодится более компактное обозначение для функций, которые являются маленькими по сравнению с какими-то другими функциями. Верный ответ.
- Перейти к основному содержанию. Вы используете гостевой доступ Вход.
- Теорема


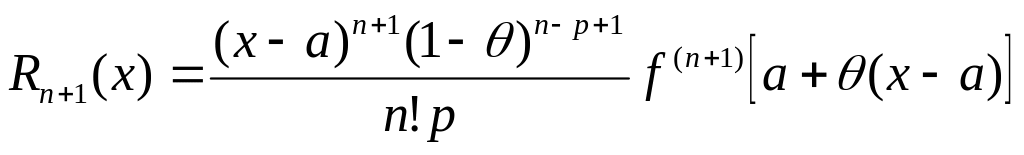


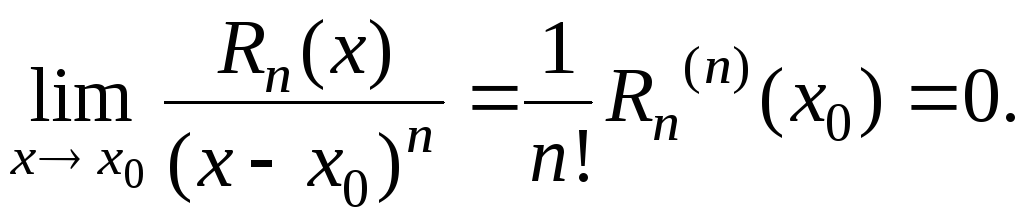

Формула называется формулой Тейлора с центром в точке a; - остаточный член в формуле Тейлора в общем виде. Рассмотрим вспомогательную функцию. Остаточный член в форме Тейлора представляет собой б. Бесплатная лекция: " Лекция 3 " также доступна. Такую запись остаточного члена называют ост. В форме Пеано:.